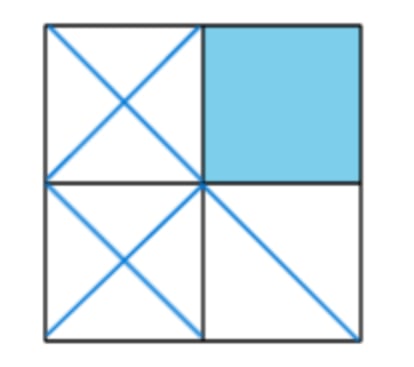
Todos hemos visto pajaritas de papel, ya sea en tres dimensiones o dibujadas, y creemos saber cómo son. Y sin embargo no es fácil dibujar una de memoria, tal como se pedía la semana pasada, a no ser que tengamos clara su estructura básica, en cuyo caso es muy sencillo: dividimos un cuadrado en cuatro cuadrados iguales, descartamos el cuarto superior derecho, trazamos una diagonal del cuarto inferior derecho y las dos diagonales de los dos cuartos restantes y… ¡voilà!, aparece ante nuestros ojos la pajarita de papel, con sus dobleces papirofléxicos y todo.
Lo difícil que a la mayoría de la gente le resulta dibujar una pajarita de papel nos dice algo sobre el funcionamiento de la memoria, que necesita apoyarse en elementos fácilmente reconocibles y con una estructura clara o un orden preciso. Esa es la clave de la mnemotecnia, que se basa en convertir una serie de elementos inconexos en un conjunto coherente y ordenado, y por ende más reconocible. Por ejemplo, para memorizar un número de teléfono de nueve cifras que, en principio (y a no ser que seas Ramanujan), no te dicen nada, como 632015150, el mnemotécnico, utilizando un método habitual, puede sustituir los dígitos por consonantes, según una tabla de conversión prestablecida (1=D, 2=N, 3=M…), para luego formar una frase fácil de recordar; en este caso, S-M-N-R-D-L-D-L-R, que, con un poco de imaginación y unas cuantas vocales añadidas, podemos convertir en algo así como “seminario del dolor”, “semanario del dólar”, “su mano ruda le dolerá”…
En cuanto al teorema de Varignon, para demostrarlo basta con recurrir al de Tales, como señala Luis Ortiz: tanto el lado HG como el EF son la mitad de la diagonal AC y paralelos a ella (ver figura correspondiente de la entrega anterior), y, análogamente, GF y HE son la mitad de la diagonal DB y paralelos a ella, por lo que EFGH es un paralelogramo, y su perímetro es igual a la suma de las diagonales del cuadrilátero inicial.
Salva Fuster aporta otra demostración menos sencilla, pero no por ello menos interesante: “Se me ocurre que para demostrar el teorema de Varignon podríamos hacer una teselación del plano con un cuadrilátero cualquiera. Para ello podemos hacer las simetrías centrales del cuadrilátero respecto a los puntos medios de sus lados, y para cada nuevo cuadrilátero seguir haciendo lo mismo. Una rápida inspección a los ángulos de cada vértice permite ver que es posible. La teselación consiste en el mismo cuadrilátero rotado y desplazado. Si extendemos los segmentos que unen los lados contiguos del cuadrilátero original se forman rectas que contendrán los puntos medios de los nuevos cuadriláteros. Además, estas rectas se podrán dividir en dos conjuntos, cada uno formado por rectas que poseen la misma dirección. Si no hubiese únicamente dos conjuntos de rectas paralelas, es decir, si los segmentos opuestos que unen los puntos medios del cuadrilátero original no fuesen paralelos, las rectas se cortarían, pero eso no sería posible”.
Por lo que respecta a los distintos problemas papirofléxicos de división del cuadrado, remito a mis pacientes lectoras/es a la sección de comentarios de la semana pasada.
Coloreando cuadrados
No se puede dividir un cuadrado en cuatro partes y trazar sus diagonales sin pensar en los cuadrados de MacMahon, un rompecabezas creado hace cien años por el matemático británico Percy Alexander MacMahon (1854-1929). MacMahon partió de un cuadrado dividido por sus dos diagonales en cuatro triángulos isósceles rectángulos, que coloreó utilizando tres colores, rojo, azul y amarillo, de todas las maneras distintas posibles (¿cuántas son?). Y a partir de ahí ideó una serie de variopintos (nunca mejor dicho) e instructivos pasatiempos geométricos. Pero ese es otro artículo…